最近在做DC竞赛上面的房价预测,因为题目要求用回归分析,而数据自变量有13列,因此采用多元回归分析。 在上网搜索过资料后,决定先分别用linearRegression和Statsmodels做一下看看效果。 之后有空会补上逐步回归的试验过程。
画图
先画散点图,看看数据的关系。
代码如下:
import xlrd
import matplotlib.pyplot as plt
import numpy as np
data = np.loadtxt(open(r'C:\Users\LENOVO\Desktop\kc_train.csv','r'), delimiter =",",skiprows=0)
#在Python中\是转义符,\u表示其后是UNICODE编码,因此\User在这里会报错,在字符串前面加个r表示就可以了
for i in range(3,14):
plt.subplot(2,6,(i-2)) #12个自变量,循环画子图
plt.scatter(data[:,i],data[:,1])
plt.title('x= %d'%i)
plt.show()
效果如下:

建立回归模型
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
def linr(dtrain,dres,ztest):
xtrain,xtest,ytrain,ytest = train_test_split(dtrain,dres,test_size=.3)
#把样本随机划分成训练集和测试集,test_size测试集占样本的比例
regr=LinearRegression()
regr.fit(xtrain,ytrain) #利用划分好的训练集进行回归
ypred = regr.predict(xtest) #对测试集进行预测
zpred = regr.predict(ztest)
MSE2 = mean_squared_error(ytest, ypred) #题目以平武预测误差为评判标准,在此查看平均预测误差
return (MSE2,zpred)
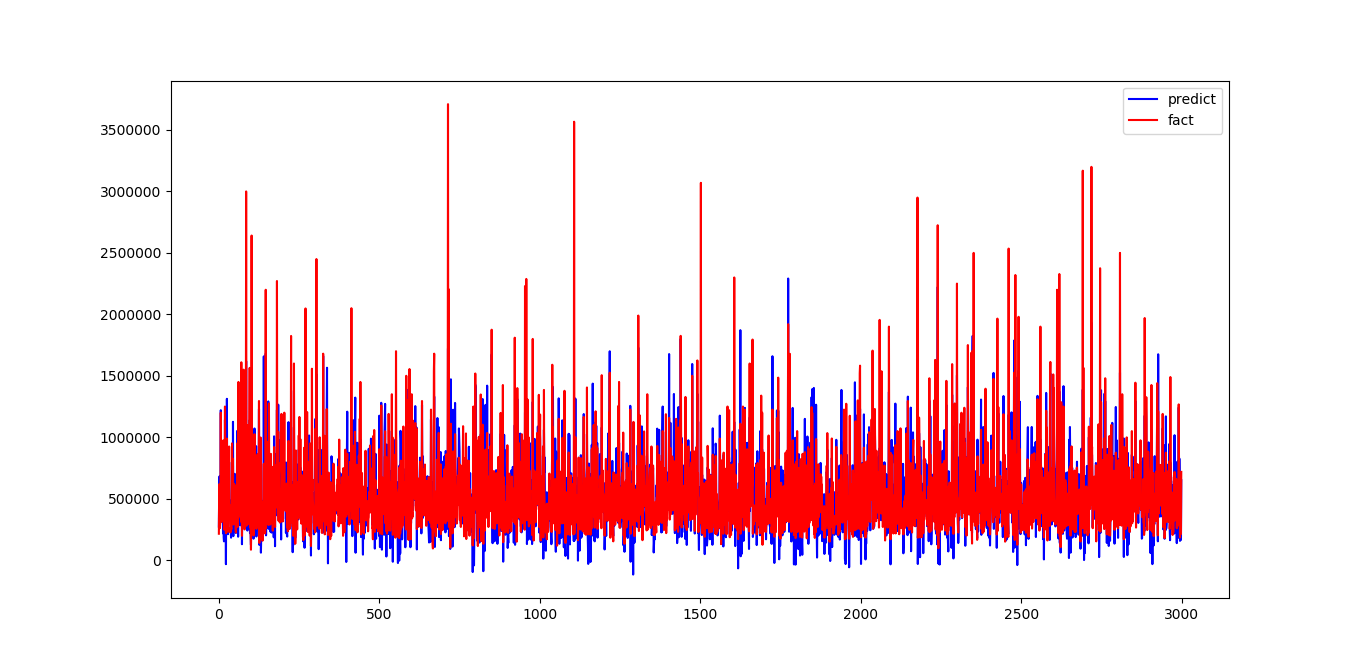
当然为了查看拟合效果,最直接的还是看图。
plt.figure()
plt.plot(ypred,'b',label = "predict")
plt.plot(ytest,'r',label = "fact")
plt.legend(loc = "upper right")
plt.show()
正是通过看图,才发现了,不对数据分段,直接拟合的话,高房价的根本无法预测出来。
数据处理及完整模型构建
因为发现高房价的无法预测,所以决定对数据分段回归。而且发现房价的高低主要受房屋面积的影响,因此,先对训练数据依据房价划分三段:(分两段和分三段都试过,但发现分三段的效果好很多。但是即使分了三段,高于500万的房价还是不能很好的拟合,说明高房价的预测需要综合很多因素,估计需要对因素设置权重,或者需要把经纬度具现化,根据房屋地段来设置权重。)
房价低于200万的,房价居于200万与500万之间的,高于500万的。
发现房屋面积的分水岭大概是3800和5000。因此对测试数据以房屋面积为依据划分为三段,并分别用对应的回归方程去拟合。
最后循环进行10次,分别保存在10个excel里,最后分别依据均值差取最优值。
完整代码:(把画图部分给去掉了)
import xlwt
import xlrd
from xlutils.copy import copy
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
data = np.loadtxt(open(r'C:\Users\LENOVO\Desktop\kc_train.csv','r'), delimiter =",",skiprows=0)
#在Python中\是转义符,\u表示其后是UNICODE编码,因此\User在这里会报错,在字符串前面加个r表示就可以了
dset = np.loadtxt(open(r'C:\Users\LENOVO\Desktop\kc_test.csv','r'), delimiter =",",skiprows=0) #读入数据
workbook = xlrd.open_workbook(r'C:\Users\LENOVO\Desktop\kc_test.xls')
wb = copy(workbook)
ws = wb.get_sheet(0)
z =dset[:,7]
y = data[:,1]
a = np.where((4000000>y)&(y>2000000)) #划分数据
a1 = len(a[0]) #注意,a为元组类型,想知道数据的列数,需提取数组元素后,再求长度
b = np.where(y<2000000)
b1 = len(b[0])
e = np.where(y>4000000)
e1 = len(e[0])
c = np.where((5000>=z)&(z>=3800))
c1 = len(c[0])
d = np.where(z<3800)
d1 = len(d[0])
f = np.where(z>5000)
f1 = len(f[0])
d1r = data[a,2:13].reshape(a1,11)
d1e = data[a,1].reshape(-1,1) #需要置换
d2r = data[b,2:13].reshape(b1,11)
d2e = data[b,1].reshape(-1,1)
z1r = dset[c,1:12].reshape(c1,11)
z2r = dset[d,1:12].reshape(d1,11)
d3r = data[e,2:13].reshape(e1,11)
d3e = data[e,1].reshape(-1,1)
z3r = dset[f,1:12].reshape(f1,11)
def linr(dtrain,dres,ztest):
xtrain,xtest,ytrain,ytest = train_test_split(dtrain,dres,test_size=.3)
regr=LinearRegression()
regr.fit(xtrain,ytrain)
ypred = regr.predict(xtest)
zpred = regr.predict(ztest)
MSE2 = mean_squared_error(ytest, ypred)
return (MSE2,zpred)
m = np.zeros((10,3))
for j in range(10):
[m1,z1] = linr(d1r,d1e,z1r)
m[j,0] =m1
[m2,z2] = linr(d2r,d2e,z2r)
m[j,1] =m2
for i in range(c1):
ws.write((c[0])[i], 14, str(z1[i])) #写入excel,并记录均值差
for k in range(d1):
ws.write((d[0][k]),14,str(z2[k]))
[m3,z3] = linr(d3r,d3e,z3r)
m[j,2] =m3
for i in range(f1):
ws.write((f[0])[i], 14, str(z3[i]))
wb.save(str(j)+'.xls')
print(m)