ER随机图巨片的涌现

October 2nd, 2019

MATLAB ER随机网络

ER随机图的涌现或相变性质

ER随机图的许多重要性质都是突然涌现的。对于任一给定连边概率p，要么几乎每一个G(N,p)都具有性质Q，要么都不具有。

当N趋于无穷大时，产生一个具有性质Q的ER随机图的概率为1，则称几乎每一个ER随机图都具有性质Q。

巨片的涌现

巨片的相对规模S∈[0,1]定义为巨片中所包含的节点数占整个网络节点的比例，亦即为网络中一个随机选择的节点属于巨片的概率。而计算S的式子为 $\tiny S = 1 - e^{-<k>S}$

画图可知， < 1时，S=0， > 1时，S>0意味着巨片涌现。

ER随机图的的平均度是 = p(N-1) ≈ pN，从而产生巨片的连边概率p的临界值为p = /(N-1) ≈ 1/N。

生成节点数N=100，不同连边概率的ER随机网络，观察巨片的涌现。

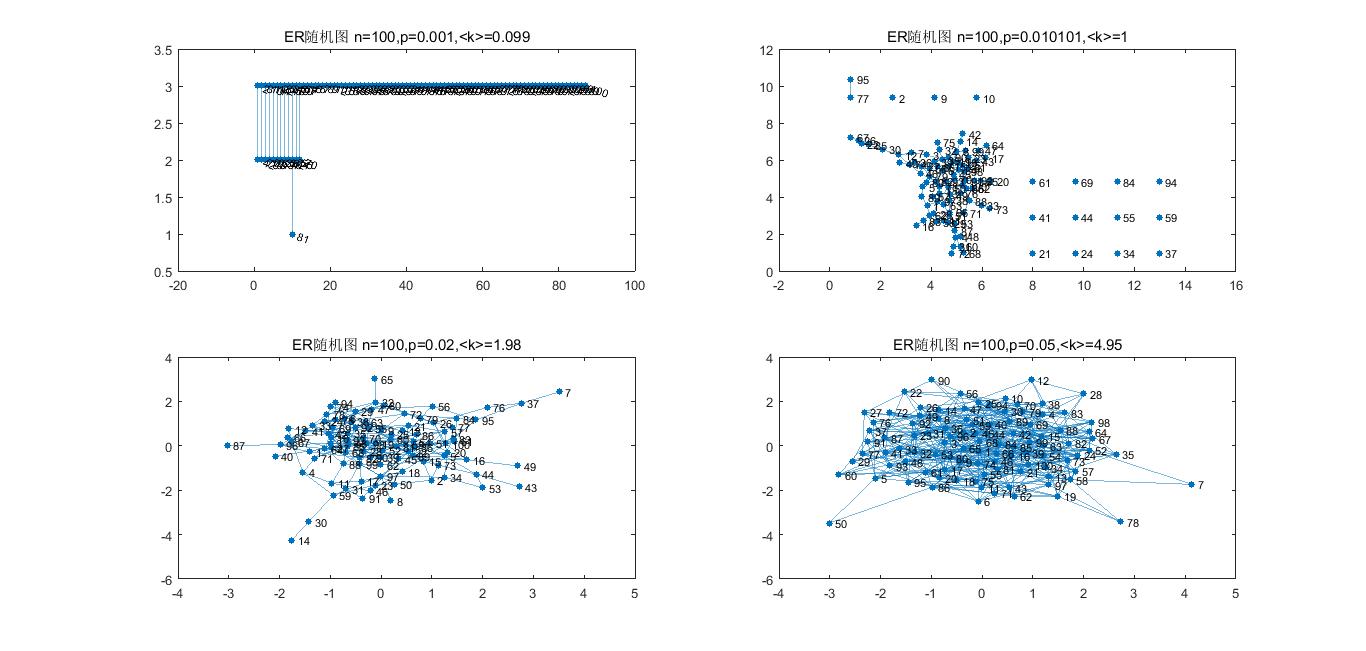
代码实现

function [  ] = testt( ~ )
n = 100;
p = [0.001,1/99,0.1,0.2];
for i = 1:4
    q = gener(n,p(i));
    j = p(i)*(n-1);
    subplot(2,2,i);
    plot(q);
    title(['ER随机图 n=',num2str(n),',p=',num2str(p(i)),',<k>=',num2str(j)]);
end
end
 
 function[z] = gener(n,p)
%UNTITLED 此处显示有关此函数的摘要
%   此处显示详细说明
a = zeros(n,n);
for i =1:n
    for j =1:n
        if i ~=j
            b = rand;
            if b < p
                a(i,j) = 1;
                a(j,i) = 1;
            end
        end
    end
end